前言:算法分析考试前12个小时,老师在群里发了背包动态规划的内容,发现还是不会,垂死病中惊坐起,补一补.. 题外话,相信自己不如相信老师(逃
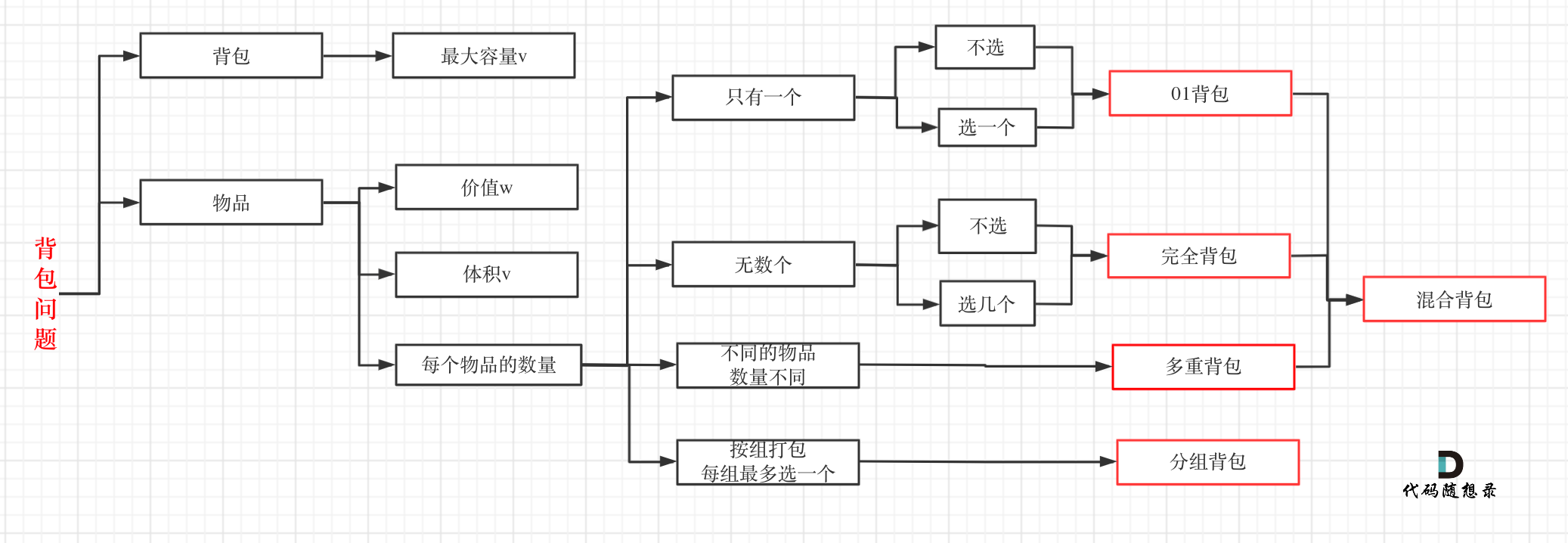
背包问题繁琐而又多样,根据所给条件不同,可以划分成不同的问题,但最后求解的目的都是一样的:如何划分使得背包总所装物品总价值最大。其中最基础的是01背包,下图可以概括基础的五种背包问题。
一、01背包
有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大?
如果使用暴力回溯,每个物品只有取和不取两种状态,则时间复杂度为O(2^n),因此必然要优化。
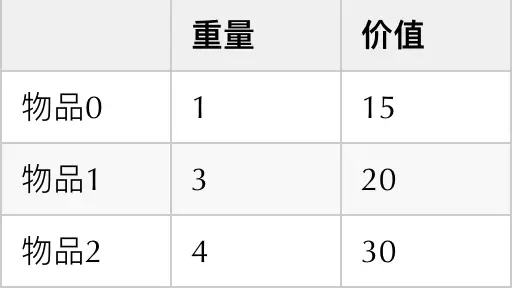
将问题具体化,假设背包最大重量W=4,物品0~2对应的weight和value如下
1、二维dp数组法
推导递归公式
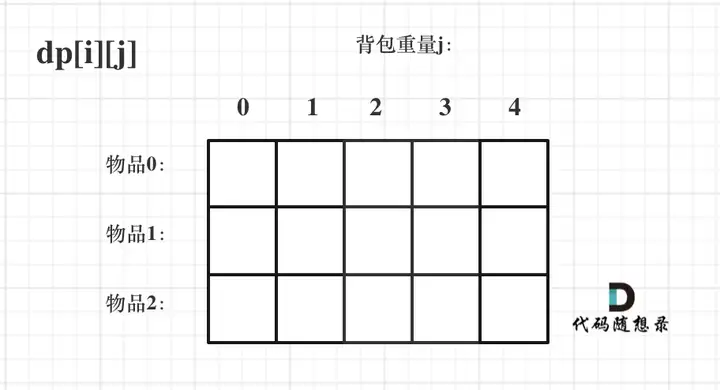
1、根据动态规划步骤,首先确定dp数组及下标含义
dp[i][j]表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大值是多少
对于如何推出dp[i][j]
- 由
dp[i-1][j]推出,即背包最大容量为j,里边不放物品i的最大价值,此时dp[i][j]=dp[i-1][j] - 由
dp[i-1][j-weight[i]]推出,dp[i-1][j-weight[i]]为背包容量为j-weight[i]时不放物品i的最大价值,那么dp[i-1][j-weight[i]]+物品i的价值value[i]就是背包放物品i时得到的最大价值
所以递归公式 dp[i][j]=max( dp[i-1][j],dp[i-1][j-weight[i]]+value[i]] )
初始化dp数组
确定递归公式后,要将dp数组初始化(牢记:**dp[i][j]表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大值是多少**)
观察可得dp[i][0]均为0
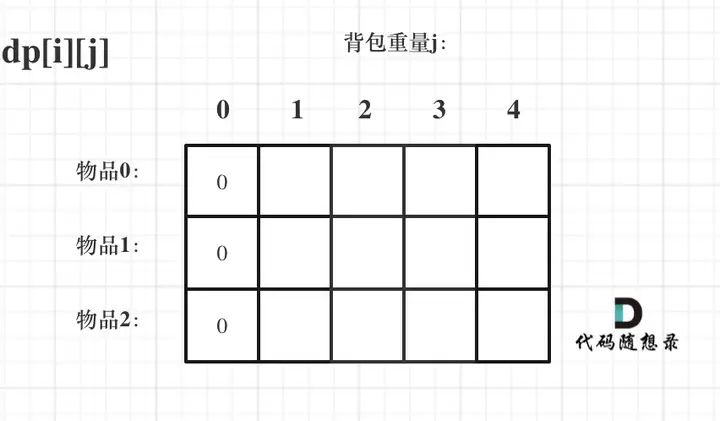
则求出dp[0][j]
//正序遍历
for(int j=weight[0];j<bagWeight;j++){
dp[0][j]=value[0];
}
此时
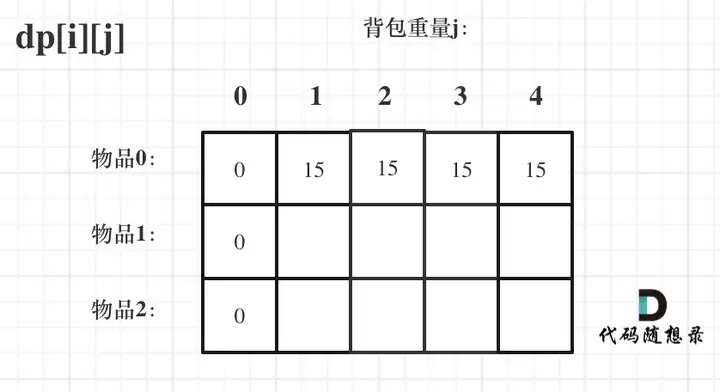
dp[0][j]和dp[i][0]已经确定,则将其他位置初始化为0即可
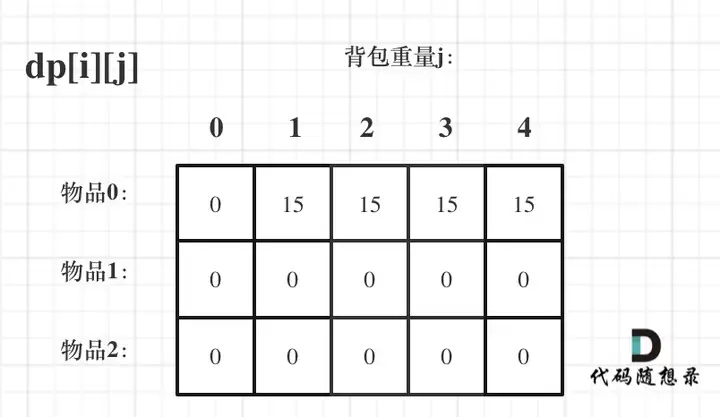
可以选择先遍历物品也可以先遍历背包重量,即谁在内循环谁在外循环均可,但先遍历物品更好解。
//weight数组的大小 就是物品的个数
for(int i=1;i<weight.size();i++){ //遍历物品
for(int j=0;j<bagWeight;j++){ //遍历背包容量
if(j<weight[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max( dp[i-1][j],dp[i-1][j-weight[i]]+value[i]] );
}
}
如果遍历背包,则
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max (dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
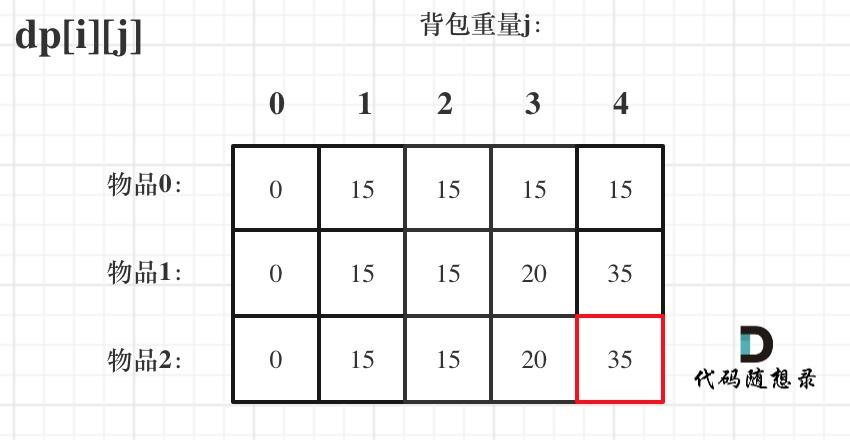
虽然两种遍历顺序有不同的地方(?),但最终都得到了相同的dp数组
最终得到dp数组
完整代码
咱就把0-1背包问题讲个通透! - 知乎 (zhihu.com)